You are here
What is Mathematical Proficiency?
Instructional Support Menu
How we think about proficiency in mathematics has varied across time, place, and context. In the early 20th century, mathematical proficiency usually referred to skill with arithmetic. In the post-Sputnik era, views on mathematical proficiency grew to include understanding the structure of mathematics and its connecting ideas. Reforms of the 1980s and 1990s emphasized mathematical problem solving, which has been refined to include goals for fluency with data, mathematical modeling, and the communication of mathematical ideas and results.
The Five Strands of Mathematical Proficiency
In the landmark publication Adding it Up: Helping Children Learn Mathematics (2001), the National Research Council (NRC) defined five “strands” of mathematical proficiency:
- Conceptual Understanding: Comprehension of mathematical concepts, operations, and relations,
- Procedural Fluency: Skill in carrying out procedures flexibly, accurately, efficiently, and appropriately,
- Strategic Competence: Ability to formulate, represent, and solve mathematical problems,
- Adaptive Reasoning: Capacity for logical thought, reflection, explanation, and justification, and
- Productive Disposition: Habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy (p. 116).
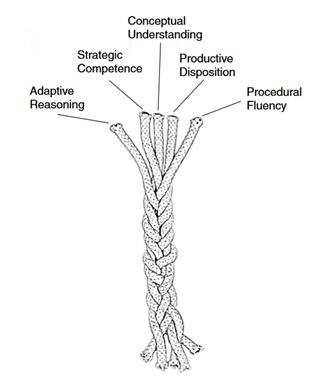
Intertwined strands of proficiency (NRC, 2001, p. 117).
To emphasize the intertwined nature of these five strands, the NRC adopted the metaphor of a braided rope. This emphasizes that mathematical proficiency depends on interdependent knowledge, skills, abilities, and beliefs.
Conceptual Understanding
Conceptual understanding refers to “an integrated and functional grasp of mathematical ideas” (NRC, 2001, p. 118). This includes knowing facts and methods, but also why those facts and methods are important and how they are connected. Students sometimes develop conceptual understanding before they can adequately verbalize it, so a teacher needs to look at how students represent mathematical situations. The ways students use and connect multiple representations of mathematical ideas are an indication of their conceptual understanding.
Procedural Fluency
Procedural fluency refers to “knowledge of procedures, knowledge of when and how to use them appropriately, and skills in performing them flexibly, accurately, and efficiently” (NRC, 2001, p. 121). Conceptual understanding and procedural fluency are sometimes seen as competing for attention when they are really two closely related, interwoven strands. Conceptual understanding makes learning skills easier, less error-prone, and easier to remember, while procedural fluency can help develop and strengthen conceptual understanding. Procedural fluency includes basic computation and estimation strategies, such as computing with whole numbers, multiplying by multiples of ten or powers of ten, and using mental strategies (like knowing that 98+37 is the same as 100+35) without the use of additional tools or technology.
Strategic Competence
Strategic competence refers to “the ability to formulate mathematical problems, represent them, and solve them” (NRC, 2001, p. 124). In school settings, students are given problems to solve and, quite often, the exact procedure needed to solve them. This is rarely how mathematics is encountered in the world, where often the greatest challenge is understanding what the problem is and deciding on a mathematical approach to solving it. To develop strategic competence, students need experience and practice with unfamiliar problem situations so they can formulate strategies and try different problem-solving approaches. This is often described as mathematical modeling, which is a process that “uses mathematics to represent, analyze, make predictions, or otherwise provide insight into real-world phenomena” (COMAP & SIAM, 2016, p. 8).
Adaptive Reasoning
Adaptive reasoning refers to “the capacity to think logically about the relationships among concepts and situations” (NRC, 2001, p. 129). This includes being able to justify valid approaches and conclusions, and it connects the many facts, procedures, concepts, and methods in ways that make sense. Even the youngest students are capable of some level of reasoning, provided that they have sufficient knowledge, the task is understandable, and the context is familiar and motivating. Justifications in mathematics can be very formal, such as in rigorous proofs, or less formal, where students provide sufficient reasons for their choices and conclusions. Adaptive reasoning takes time to develop. Students need regular opportunities to talk about the concepts and procedures they are using and the reasons for what they are doing.
Productive Disposition
Productive disposition refers to “the tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics” (NRC, 2001, p. 131). For students to develop conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning, they need a productive disposition towards mathematics. Likewise, students’ productive disposition will improve as they develop conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning. Most children enter school with positive attitudes towards mathematics, but to sustain those beliefs, students need reinforcement that math ability is not a fixed trait, that math is about reasoning and sensemaking, and that everyone – regardless of background – can be a capable doer of mathematics.
Developing Mathematical Proficiency
Mathematical proficiency is not an “all or none” trait. Even before formal instruction, students bring with them understandings about mathematical ideas, and each idea can be understood in different ways and at different levels. Mathematical proficiency develops over time, and development of each of the five strands of mathematical proficiency might develop unevenly. It is challenging for teachers to see that students are making progress along every strand, and to develop activities for students to help them bring all five strands of mathematical proficiency up to a high level for every mathematical idea and every student. According to the NRC, “Students should not be thought of as having proficiency when one or more strands are undeveloped” (2001, p. 135).
Evidence from the National Assessment of Educational Progress (NAEP) and other assessments show that students in the U.S. develop mathematical proficiency unevenly, typically with better performance in procedural fluency than the other four strands. For example, many students can add and subtract multidigit numbers, but fewer students can construct multidigit numbers when given digits and their place values. Similarly, students can often compute with decimal numbers and fractions, but struggle to put those numbers in order from least to greatest. These are signs of weaknesses in students’ conceptual understanding. For strategic competence, U.S. students have long shown increased difficulty when faced with problem-solving situations. Although they may add or subtract two- and three-digit numbers with high rates of success, their success on addition and subtraction word problems is much lower, especially if there is more than one step required for a solution or a need to dismiss extraneous information. Adaptive reasoning tasks include problems like, “If 37+61=98 is true, is 98-61=37 also true?” Students have lower success on tasks of this type compared to those simply asking them to compute a result. Justifications of mathematical reasoning are often difficult for students, which is another sign of weakness in adaptive reasoning. Finally, problems with productive disposition towards mathematics are well-known, both for students and, generally, the public at large. On past NAEP surveys, about 70% of students agree that mathematics is useful for solving everyday problems, yet, as the NRC summarized, “Although students appear to think mathematics is useful for everyday problems or important to society in general, it is not clear that they think it is important for them as individuals to know a lot of mathematics” (2001, p. 141).
References
COMAP & SIAM. (2016). GAIMME: Guidelines for assessment & instruction in mathematical modeling education (p. 220). Consortium for Mathematics and Its Applications and the Society for Industrial and Applied Mathematics.
National Research Council. (2001). Adding it up: Helping children learn mathematics (J. Kilpatrick, J. O. Swafford, & B. Findell, Eds.). National Academy Press.


Connect With Us





